| Introduction to Design Theory |
| Design Objectives |
| Searching for the Best Design |
| ASD vs LRFD |
| Example Problems |
|
References |
| Report Errors or Make Suggestions |
| Make Donation |
Section DC.5
ASD vs LRFD
Last Revised: 11/04/2014
When designing in steel and timber, there is choice of design philosophies that needs to be made. In concrete the only design philosophy in extensive use is strength based (LRFD).
Steel
Before getting too deep into this section, it would be wise for your to read the AISC Steel Construction Manual (SCM) sections describing the Load and Resistance Factor Design and Allowable Strength Design philosophies as well as the section on Design Fundamentals. These are found on pages of 2-6 and 2-7 of the SCM.
Until AISC introduced the Load and Resistance Factor Design (LRFD) specification in 1986, the design of steel structures was based solely on Allowable Stress Design (ASD) methodologies. The shift to LRFD has not been readily embraced by the profession even though almost all universities shifted to teaching the LRFD specification within ten years of its introduction. Its seems that there was not a perceived need by the profession to change methodologies even though there was ample evidence that LRFD produced structures with a more consistent factor of safety.
Timber
LRFD is relatively new to timber. It was explicitly included with ASD in the National Design Specification with the latest edition of the specification.
Concrete
Because of the complexities of analyzing composite sections using working stress method, the much simpler strength approach was easily adopted with it was first introduced. The strength based (LRFD) method has been in use in the concrete specification ACI 318 since the 1970s.
There were two major differences between the two specifications:
- The comparison of loads to either actual or ultimate strengths and
- a difference in effective factors of safety.
Actual vs. Ultimate Strength
|
Figure DC.5.1 |
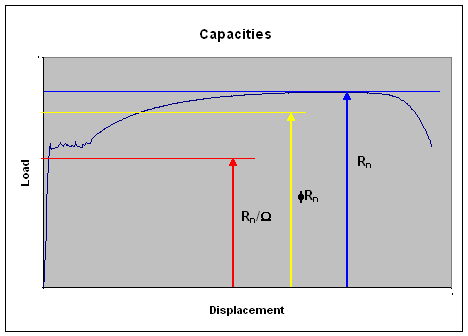 |
|
Rn/
W= ASD Capacity |
The first difference between ASD and LRFD, historically, has been that the old Allowable Stress Design compared actual and allowable stresses while LRFD compares required strength to actual strengths. The difference between looking at strengths vs. stresses does not present much of a problem since the difference is normally just multiplying or dividing both sides of the limit state inequalities by a section property, depending on which way you are going. In fact, the new AISC Allowable Strength Design (ASD), which replaces the old allowable stress design, has now switched the old stress based terminology to a strength based terminology, virtually eliminating this difference between the philosophies.
Figure DC.5.1 illustrates the member strength levels computed by the two methods on a typical mild steel load vs. deformation diagram. The combined force levels (Pa, Ma, Va) for ASD are typically kept below the yield load for the member by computing member load capacity as the nominal strength, Rn, divided by a factor of safety, W, that reduces the capacity to a point below yielding. For LRFD, the combined force levels (Pu, Mu, Vu) are kept below a computed member load capacity that is the product of the nominal strength, Rn, times a resistance factor, f.
When considering member strengths, we always want to keep our final design's actual loads below yielding so as to prevent permanent deformations in our structure. Consequently, if the LRFD approach is used, then load factors greater than 1.0 must be applied to the applied loads to express them in terms that are safely comparable to the ultimate strength levels. This is accomplished in the load combination equations that consider the probabilities associated with simultaneous occurrence of different types of loads.
Fixed vs. Variable Factors of Safety
The second major difference between the two methods is the manner in which the relationship between applied loads and member capacities are handled. The LRFD specification accounts separately for the predictability of applied loads through the use of load factors applied to the required strength side of the limit state inequalities and for material and construction variabilities through resistance factors on the nominal strength side of the limit state inequality. The ASD specification combines the two factors into a single factor of safety. By breaking the factor of safety apart into the independent load and resistance factors (as done in the LRFD approach) a more consistent effective factor of safety is obtained and can result in safer or lighter structures, depending on the predictability of the load types being used.
Load Combination Computations
The basis for structural load computations in the United States is a document known as ASCE 7: Minimum Design Loads for Buildings & Other Structures. (See A Beginner's Guide to ASCE 7-05 for detailed discussion about this document.) Typically, each load type (i.e. dead, live, snow, wind, etc) are expressed in terms of their service load levels. The one exception to this is earthquake loads, which are expressed at strength levels. The individual loads are then combined using load combination equations that consider the probability of simultaneously occurring loads. The resulting combined loads and load effects from LRFD combinations equations are given subscript of "u". A subscript of "a" is used to indicate a load result from an ASD load combination. Particular to this text, a subscript of "s,equiv" is used to represent the result of a load combination that is the simple algebraic sum of all the individual load components.
Load factors are applied as coefficients in the load combination equations for both ASD and LRFD. The resistance factor is denoted with the symbol f, and the factors of safety with the symbol W. We'll see how they are applied below.
The other issue that seems to be conceptually challenging for many engineers is that, since LRFD looks at the strength of members (i.e. the loads that cause failure) the "applied" loads are "fictitiously" increased by a load factors so that they can be safely compared with the ultimate strengths of the members. Throughout these notes and the specification loads that have had LRFD load factors applied (and are higher than they will actually be) are called ULTIMATE or FACTORED loads. ASD loads that are the result of ASD load combination equations are also FACTORED loads. Loads at their actual levels are referred to as SERVICE loads.
Comparing LRFD and ASD Loads
Ultimate or factored loads CANNOT be directly compared with service loads. Either the service loads must be factored or the ultimate loads must be unfactored if they are to be compared. This gets even more complicated when you consider the effect on load combination equations. One method for comparing loads is to compute a composite load factor (CLF) that is the ratio of load combination result (Pu or Pa) to the algebraic sum of the individual load components (Ps,equiv or Ps,eq). The load combination with the lowest CLF is the critical load combination. The computation of CLF is shown in Table DC.5.1.
|
Table DC.5.1 |
||||||
|
||||||
Where:
|
Examples of this are given in the next section on load combinations since it is in the load combination equations where the load factors are applied.
Putting it all together, the general form of the limit state inequalities can each be expressed three ways. Table DC.5.2 shows how this is done for LRFD and ASD for four common strength limit states. Note that each equation is equivalent.
|
Table DC.5.2 |
|||||||||||||||
|
The choice of form is dependent on what you are trying to do. This will become evident as the limit states are explained and demonstrated throughout this text. In general, the second form (Req'd nominal effect < actual nominal strength) is useful when you are selecting (or designing) member for a particular application. The other two forms are useful when analyzing the capacity of a particular member.
LRFD Effective Factor of Safety
Another approach to comparing the two methods is to compute an effective factor of safety for the LRFD method that can be compared with the ASD factors of safety. This involves combining the load and resistance factors.
Let us take the axial force limit state to conduct a comparative example between ASD and LRFD. You can divide through by the load factors to get an equivalent factor of safety:
LRFD : Ps,equiv < Pn (f / CLFLRFD) = Pn/ Weff
Where the LRFD equivalent factor of safety is the term Weff = (f / CLFLRFD). f is a constant. The composite load factor, CLF = Pu/( Ps,equiv), varies with the relative magnitudes of the different types of loads. The result is a variable factor of safety for LRFD. In ASD this factor of safety is taken as a constant.
It can be argued that the variable LRFD Weff is more consistent with the probabilities associated with design. The result is that structures with highly predictable loadings (i.e. predominately dead load) the LRFD Weff is lower than the ASD W which results in a potentially lighter structure. For structures subjected to highly unpredictable loads (live, wind, and seismic loads for example) the LRFD Weff is higher than the ASD W which results in stronger structures. The LRFD argument is that ASD is overly conservative for structures with predicable loads and non conservative for those subject to less predictable loads.
Use of ASD and LRFD
Finally, you should be aware that you must select one or the other of the design philosophies when you design a structure. You cannot switch between the two philosophies in a given project! In this text we use both ASD and LRFD so that you can be conversant in both but this is not the standard in practice.