| Overview |
| Elastic Analysis |
| Plastic Analysis |
| Envelopes |
| Example Problems |
| Homework Problems |
| Report Errors or Make Suggestions |
| Make Donation |
Section CB.2.2
Finding Shear and Moment Diagrams
After Obtaining End Moments
Last Revised: 08/01/2008
For any given 2D member subjected only to transverse loads, there are four reaction components (shear and moment at each end of the FBD of the span) and two equations of equilibrium, hence the problem is statically indeterminate.
Classical methods of structural analysis (such as slope-deflection or moment distribution) or numerical methods (such as the stiffness method) can be used to solve for the end moments, thus leaving two unknown reactions and two equations of equilibrium. Thus the solution of the shears can be accomplished using equilibrium equations.
A typical FBD for a single span subjected to a uniform distributed load is given in Figure CB.2.2.1.
Figure CB.2.2.1
FBD of a Single Span Subjected to a Uniformly Distributed Load
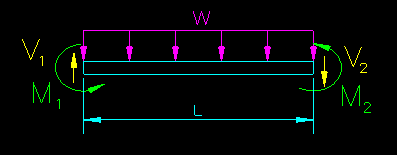
If M1 and M2 are known, then sum of moments about the right end yields:
V1 = (M1 + M2)/L + wL/2
Once V1 and M1 are known, the internal shear and moment at location "x" (see Figure CB.2.2.2) can be determined.
Figure CB.2.2.2
FBD of a Beam Segment
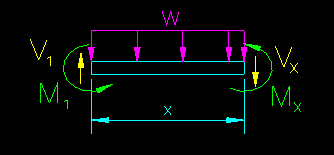
The equations for Vx and Mx are found by applying equilibrium equations:
Vx = - w x + V1
Mx = -w x2/2 + V1 x - M1
Graphing these equations along the span will result in the shear and moment diagrams for the span.
Similar equations can be derived for other loading conditions. Discontinuous loading will require more effort, but can be accomplished by anyone with a good understanding of the principles of Statics.