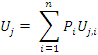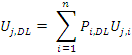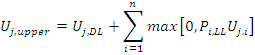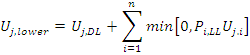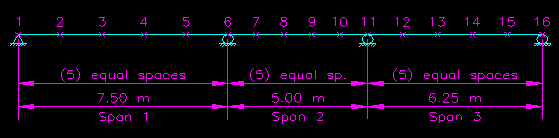| Overview |
| Elastic Analysis |
| Plastic Analysis |
| Envelopes |
| Example Problems |
| Homework Problems |
| Report Errors or Make Suggestions |
| Make Donation |
Section CB.4.1
Influential Superpostion
Last Revised: 08/01/2008
The method presented here was developed by the author to facilitate some research that required the development of many moment envelopes. It is also useful for axial force, shear and deflection envelopes as well.
As with other methods, the structural geometry is defined and the possible locations and nature (i.e. point, uniform, linearly varying, etc.) of the live loads is determined. For the method of influential superposition, unit loads of the same nature as the real live loads are applied individually to the structure and the effects on the structure are determined. To find the actual load effect the load effect due to the unit load can then be multiplied magnitude of the actual load.
The Basic Premise
As a simple example of the basic idea, consider the cantilever beam shown in Figure CB.4.1.1. The beam is subjected to a uniform load, w, and a point load P. We show these at load cases 1 and 2, respectively.
Figure CB.4.1.1
Demonstration Problem
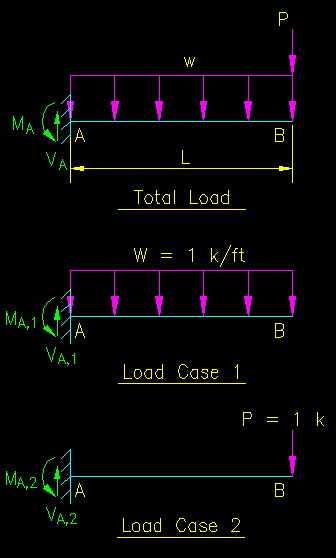
If we call the distribute load LC1 and the point load LC2 we can find the values of shear and moment at point A if each of the loads is a unit load. Set the beam length, L to 10 ft. The resulting values are:
| VA,1 = 10 k / (k/ft) | VA,2 = 1 k / k |
| MA,1 = 50 ft-k / (k/ft) | MA,2 = 10 ft-k / k |
Now that we have done the structural analysis for the two load cases, we don't need to do any more structural analysis. To find the total shear at A, we need only take the shears that resulted from the unit loads and multiply by the actual loads.
Let's say that the real beam has a distributed load that consists of 1.25 k/ft of Dead Load and 1.5 kips of Live Load and point load at B that consists of 5 kips dead load and 7 kips snow load.
The shear at A becomes:
VA = (1.25 k/ft + 1.5 k/ft) VA,1 + (5 k + 7
k) VA,2
VA
= (2.75 k/ft) (10 k/(k/ft)) + (12 k) (1 k/k)
VA = 39.5 k
And the moment at A becomes:
MA = (1.25 k/ft + 1.5 k/ft) MA,1 + (5 k + 7
k) MA,2
MA
= (2.75 k/ft) (50 ft-k/(k/ft)) + (12 k) (10 ft-k/k)
MA = 257.5 ft-k
If we find that we have another load combination that has the same load cases but different magnitudes, we are spared the trouble of doing another analysis. Eliminating the need to perform more than a minimum number of analyses is where this method finds its advantage. We simply multiply the unit load effects by the new magnitudes to get the results.
The basic equation for finding a particular load effect at a particular location on the structure becomes
|
|
(Equation CB.4.1.1) |
Where:
- Uj is the total load effect (axial, shear, moment, or deflection) at point j of the structure
- Pi is the magnitude of load case i
- Uj,i is the load effect at point j due to a unit load used for load case i
While the above example is very simplistic (and not of any real value to the simple problem given), the method becomes quite valuable when the analysis is more complex. This happens when a structure is statically indeterminate and envelopes need to be developed.
Developing Envelopes
Since load effect envelopes are built off the fixed load only case, this case is computed first.
|
|
(Equation CB.4.1.2) |
Where
- Uj,DL is the load effect at point j due to dead load (or other fixed load)
- Pi,DL is the dead load component of load case i
- n is the number of load cases (i.e. number of analyzes)
- Uj,i is the load effect at point j due to a unit load used for load case i
As an envelope shows only the upper and lower bound of the load effect, this particular method is very useful since only the live load terms with either positive or negative values (depending on if an upper or lower bound is sought) are included. This eliminates the need to compute every possible load arrangement if the primary load cases are appropriately chosen.
To find the upper bound of the load effect envelope, simply add only those load effects that have positive values:
|
|
(Equation CB.4.1.3) |
Similarly, to find the lower bound of the load effect envelope, simply add only those effects that have negative values:
|
|
(Equation CB.4.1.4) |
Where
- Ui,upper is the upper bound load effect.
- Ui,lower is the lower bound load effect
- Uj,DL is the load effect at point j due to dead load (or other fixed load)
- Pi,LL is the live (or other non fixed) load component of load case i
- n is the number of load cases (i.e. number of analyzes)
- Uj,i is the load effect at point j due to a unit load used for load case i
Example: Moment Envelope for a Three Span Continuous Beam
The method is best understood by application to an example problem. In the interest of space, a simple continuous beam problem with uniformly distributed loads is chosen and the envelope values will be determined only at points along the span, in addition the values at the supports. Geometry of the problem is shown in Figure CB.4.1.2. The sixteen points along the beam represent location where envelope values will be determined.
Figure CB.4.1.2
Example Geometry
Click on image to get larger view
A uniformly distributed dead load of 4 kN/m will be used for all spans. Uniformly live loads of 6 kN/m, 8 kN/m, and 7 kN/m will be used for spans 1, 2, and 3 respectively.
Figure CB.4.1.3 shows some the load cases (two cases are missing from the set) that might be considered in a typical analysis of the given structure. The result is that a minimum of six live load analyzes must be done and their results superimposed on the dead load case so as to determine the load effects at each point of interest. For this example the load effect, U, to be considered is bending moment, M.
Figure CB.4.1.3
Typical Load Cases
Click on image to get larger view
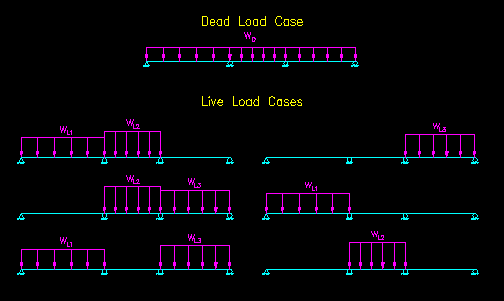
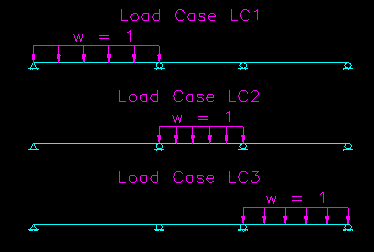
Figure CB.4.1.4 shows the load cases used by the method of influential superposition. With this method, three analyzes are run. The load cases are numbered by span. For example, LC1 is the case with the unit load only on span 1. Note that the unit load is unitless.
Figure CB.4.1.4
Basic Load Cases
Click on image to get larger view
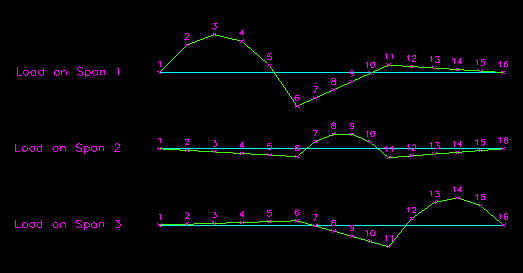
The bending moment results of the three influential superposition analyzes are given in Table CB.4.1.1 and illustrated in Figure CB.4.1.5. These results can be obtained by any means of classical or numerical analysis. Since the unit load has no units, the results are in units of m2.
Table CB.4.1.1
Moments Resulting From Unit Loads
| Point | LC1 | LC2 | LC3 |
| (m2) | (m2) | (m2) | |
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | 3.62 | -0.20 | 0.11 |
| 3 | 4.98 | -0.41 | 0.23 |
| 4 | 4.10 | -0.61 | 0.34 |
| 5 | 0.97 | -0.81 | 0.45 |
| 6 | -4.41 | -1.02 | 0.57 |
| 6 | -4.41 | -1.02 | 0.57 |
| 7 | -3.34 | 0.95 | -0.11 |
| 8 | -2.26 | 1.92 | -0.79 |
| 9 | -1.18 | 1.90 | -1.48 |
| 10 | -0.10 | 0.87 | -2.16 |
| 11 | 0.98 | -1.16 | -2.84 |
| 11 | 0.98 | -1.16 | -2.84 |
| 12 | 0.78 | -0.93 | 0.85 |
| 13 | 0.59 | -0.70 | 2.98 |
| 14 | 0.39 | -0.47 | 3.55 |
| 15 | 0.20 | -0.23 | 2.56 |
| 16 | 0.00 | 0.00 | 0.00 |
Figure CB.4.1.5
Moment Diagrams from Unit Load Cases
Click on image to get larger view
Three combinations are now required. The first is the combination for the dead load case and the other two are the lower and upper bounds of dead plus live load. For illustration, we will look at moment at point 6 (i.e. i=6). The same can be done at all other points.
The dead load case is computed by equation CB.4.1.2.
M6,DL = SUM {from i=1 to 3} (P1,DL M6,i)
M6,DL = 4 kN/m * (-4.41 m2) + 4 kN/m * (-1.02 m2) + 4 kN/m * (+0.57 m2)
M6,DL = 4 kN/m * (-4.86 m2)
M6,DL = -19.46 Kn-m
This equation includes the moment contribution of loads on all of the spans, regardless of sign. All span effects are included since dead load is always everywhere present at the same time and all spans contribute to the moment at point 6. M6,DL is the moment at point 6 when the dead load is applied to all spans.
The lower and upper bounds, Mlower,i and Mupper,i, are determined from equations CB.4.1.3 and CB.4.1.4.
M6,upper = M6,DL + wL1 * max (0,M6,1) + wL2 * max(0,M6,2) + wL3 * max(0,M6,3)
M6,upper = -19.46 kN-m
+ 6 kN/m * max (0,-4.41 m2)
+ 8 kN/m * max(0,-1.02 m2)
+ 7 kN/m * max(0,0.57 m2)
M6,upper = -19.46 kN-m + 6 kN/m * 0 + 8 kN/m * 0 + 7 kN/m * 0.57 m2
M6,upper = -19.46 kN-m + 3.97 kN-m
M6,upper = -15.49 kN-mM6,lower = M6,DL + wL1 * min (0,M6,1) + wL2 * min(0,M6,2) + wL3 * min(0,M6,3)
M6,lower = -19.46 kN-m
+ 6 kN/m * min (0,-4.41 m2)
+ 8 kN/m * min(0,-1.02 m2)
+ 7 kN/m * min(0,0.57 m2)
M6,lower = -19.46 kN-m + 6 kN/m * (-4.41 m2) + 8 kN/m * (-1.02 m2) + 7 kN/m * 0
M6,lower = -19.46 kN-m - 34.63 kN-m
M6,lower = -54.09 kN-m
Note how the live load magnitudes are applied. To get the moment at point i due to load case LCj, multiply the moment at point i due to the unit load in LCj by the actual load applied at the same location as the unit load used in LCj. In the above sample, a unit load on span 1 (LC1) causes a moment of -4.41 m2 at point 6. To get the moment due an applied load of 6 kN/m on span 1, multiply the moment from the unit load (-4.41 m2) by the applied load magnitude. Similarly to get the moment contribution at point 6 due to an applied load of 8 kN/m on span 2, multiply the moment resulting from the unit load (-1.02 m2) by the actual load applied to the span (8 kN/m).
Examining the equation for computing the upper bound, note that the terms associated with load on spans 1 and 2 are zero. This results from the maximum statement in equation CB.4.1.2. The moment at point 6 due to the load on spans 1 and 2 are negative and, as such, do not contribute to the upper bound moment. Similarly for the lower bound calculation, the term associated with load on span 3 is taken as zero since the resulting moment for the associated load case is positive and does not contribute to the lower bound. The end effect is that only spans 1 and 2 are loaded with live load for the lower bound and only span 3 is loaded with live load for the upper bound. These load arrangements are two of the load arrangements predicted by drawing the influence line for moment at point 6, however the explicit step of determining the arrangements via influence line determination is not necessary since the method picks up on which load cases are applicable.
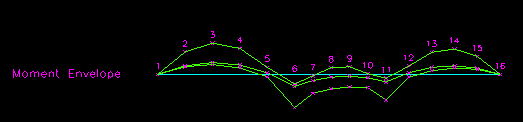
Similar calculations are made for the other points of interest. The results are tabulated in Table CB.4.1.2 and illustrated in Figure CB.4.1.6. Slight differences between that results in the sample calculation and Table 2 result from round off error. Careful observation of Figure CB.4.1.6 and the data in Tables CB.4.1.1 and CB.4.1.2 reveal that the upper and lower envelope values come from different live load arrangements. Other methods would require the analysis of all the different load arrangements to get the same results.
Table CB.4.1.2
Moment Envelope Values
| Point | DL | Upper | Lower |
| (kN-m) | (kN-m) | (kN-m) | |
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | 14.11 | 36.60 | 12.48 |
| 3 | 19.22 | 50.71 | 15.96 |
| 4 | 15.32 | 42.31 | 10.44 |
| 5 | 2.43 | 11.42 | -4.08 |
| 6 | -19.46 | -15.49 | -54.09 |
| 6 | -19.46 | -15.48 | -54.09 |
| 7 | -9.98 | -2.36 | -30.79 |
| 8 | -4.51 | 10.89 | -23.61 |
| 9 | -3.03 | 12.13 | -20.43 |
| 10 | -5.56 | 1.37 | -21.25 |
| 11 | -12.08 | -6.19 | -41.25 |
| 11 | -12.08 | -6.20 | -41.26 |
| 12 | 2.83 | 13.52 | -4.61 |
| 13 | 11.50 | 35.92 | 5.92 |
| 14 | 13.92 | 41.13 | 10.20 |
| 15 | 10.08 | 29.16 | 8.22 |
| 16 | 0.00 | 0.00 | 0.00 |
Figure CB.4.1.6
Resulting Moment Envelope
Click on image to get larger view
Summary
The same approach used here for moment envelope determination could also be used to determine shear or deflection envelopes for the same structural system. The method can also be used with arrangements of point loads and moments as well as distributed loads on more complex structures. It can be used whenever superposition is applicable.
The method of Influential Superposition can be used to reduce the number of analyzes required for the determining envelopes of continuous structures. The method can be easily implemented in numerical analysis programs in order to reduce the number of load cases to be developed by the user and to reduce the computational effort.
The method has the added advantage of reducing the potential for inadvertent neglect of all applicable live load arrangements.