BGASCE7-10 Section 6.7.3
Example Problem 6.3
Last Revised: 11/04/2014
Given: The two buildings depicted in Figures 6.7.1 & 6.7.2 and the criteria given for the chapter 6 example problems.
Wanted: Determine the breaking wave and hydrostatic pressure distributions on the structural elements for both buildings plus the total net force on each wall or piling.
Solution: There is are different ASCE 7-10 sections for the two cases shown here.
Option 'A' Building
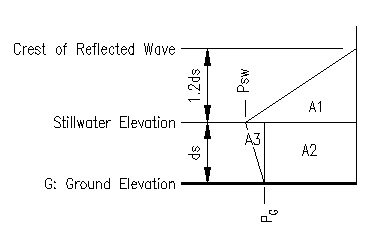
The pressure diagram for a breaking wave on a wall is given in ASCE 7-10 Figure 5.4-1. The key defining terms of the diagram are the stillwater depth, overall height (2.2ds), the pressure at the stillwater depth (ASCE 7-10 equation 5.4-5). and the pressure at the ground surface (g*overall depth).
To compute the pressure at still water depth, the building category is needed to determine the Dynamic Pressure Coefficient (Cp) from ASCE 7-10 Table 5.4-1. As this is a utility building and not considered to be essential in any way, we can classify the building as Category I (see ASCE 7-10 Table 1.5-1). This gives us a Cp of 1.6.
For this problem, the values are:
Stillwater depth, ds = 3.25 ft (computed in a previous problem)
Overall height, 2.2ds = 7.15 ft
Pressure at stillwater depth = [1.6 + 1.2](3.25 ft)(64.0 pcf) = 582 psf
Pressure at ground surface = (64.0 pcf)(2.2)(3.25 ft) = 458 psf
Figure 6.7.3.1 shows one way to define the pressure diagram. It has been done in this way in order to easily numerically integrate the area and find it's centroid. The resultant force acts through the center of the shown area. Table 6.7.3.1 shows the spreadsheet computation performed to obtain the resultant force and vertical location.
Figure 6.7.3.1
Breaking Wave on a Wall Pressure Distribution

Table 6.7.3.1
Force and Centroid Computation
| Force | Arm | Moment | |
| (lb) | (ft) | (ft-lb) | |
| A1 | 1135.7 | 4.55 | 5167 |
| A2 | 1487.2 | 1.63 | 2417 |
| A3 | 202.8 | 2.17 | 439 |
| Total | 2825.7 | 2.84 | 8023 |
The resultant force per unit length of wall is 2,826 lb/ft of
wall
The resultant force is applied 2.84 ft above the eroded ground surface
The force on the long and short walls can now be computed:
Force on long wall = (2,826 lb/ft) (20 ft) = 56.5 kips
Force on the short wall = (2,826 lb/ft) 120 ft) = 28.3 kips
A quick comparison with the results of the non-breaking wave load computed in example problem 6.2 (21.7 k and 10.8 k) quickly shows that breaking wave create significantly larger forces than non-breaking waves.
You can reduce these forces on each wall by considering water inside the building. You would subtract the stillwater hydrostatic force computed in example problem 6.1.
The total lateral force on the building in each direction can be computed by taking these breaking wave forces and subtracting the hydrostatic external forces computed in example problem 6.1.
Net lateral force in the short direction = 56.5 k - 16.0 k =
40.5 kips
Net lateral force in the long direction = 28.3 k - 8.0 k = 20.3 kips
Option 'B' Building
Computing the force on the piling involves ASCE 7-10 equation 5.4-4. For this equation we need a breaking wave drag coefficient, CD, diameter of the pile, D, and the height of the breaking wave, Hb. The Standard does not provide a pressure distribution for breaking waves on piling.
Hb is computed using ASCE 7-10 equation 5.4-2:
Hb = 0.78ds = 0.78 (3.25 ft) = 2.54 ft
D is the pile diameter in feet for a round pile. If the pile is square or rectangular, it is largest exposure dimension (generally the diagonal across the member). In our case, we have a round pile and
D = 8" = 0.667 ft
CD is given in ASCE 7-10 5.4.4.1. For our round pile
CD = 1.75
With this information, we can compute the force on a single pile based on a breaking wave.
FD = 0.5 (64.0 pcf) (1.75) (0.667 ft) (2.54 ft)2 = 240 lb / piling
There are six (6) piling, so the total force on the structure due to breaking waves is:
FDtotal = (6 piling) (240 lb/piling) = 1,440 lbs = 1.44 kips
Solution Summary:
Option A:
Option B:
A quick comparison of results shows the impressive difference in the forces on these two types of construction to be built at the same location. From a cursory glance it appears that the piling alternative is quite attractive and should be considered.
In this case, tsunami hydrodynamic forces are comparable to breaking wave forces on building option 'A'. In both cases, the force levels are quite unreasonable to design for. It would be a good idea to not construct this building where it would be exposed to breaking waves or tsunami runup.