A Beginner's Guide to ASCE 7-05

Chapter 2 - Load Combinations

© 2007, 2009, T. Bartlett Quimby

Overview

The Load Combination Equations
Comparing LRFD & ASD Results

Example Problems

Homework Problems

References
Report Errors or Make Suggestions

 

Section 2.3

Comparing LRFD & ASD Results

Last Revised: 11/04/2014

LRFD and ASD loads are not directly comparable because they are used differently by the design codes.  LRFD loads are generally compared to member or component STRENGTH whereas ASD loads are compared to member or component allowable values that are less than the full strength of the member or component.  In order to determine which design philosophy is more or less demanding (i.e. results in larger members), it is necessary to "unfactor" the load combinations using the material specific strength and allowable stress requirements. 

Also, there are times when you will know the capacity of a member relative to a limit state and want to know what actual loads you can put on it.  In order to accomplish this task you need to "turn around" the load combination equations and compute D, L, etc.  To accomplish this task, you will need to know the relative magnitudes of the service load (i.e. actual applied magnitudes) components.  This tends to get extraordinarily difficult if your member has multiple load sources (i.e. a uniform load, a point load, etc.), however if you have a single load source the task is manageable.

This text uses a service level equivalent load, Ps,equiv (or Ps,eq), for comparison of LRFD and ASD loads.  The equivalent service load is taken to be the sum of all service level load components extracted from a particular load combination equation.  The next section illustrates this concept using the requirements of the 13th edition of the AISC Steel Construction Manual.

Converting Load Combinations to a Comparable Equivalent Load

The typical strength based limit state statement takes the form:

LRFD ASD
Pu < fPn Pa < Pn/ W

Where Pu and Pa are values of design loads that have been computed using the load combination equations and the terms on the right side of each equation represent the capacity of the member. 

For example, let us assume that we know the axial force capacity of a tension member and that the applied dead load equals the live load and the seismic load is twice the dead load.  In other words, the load consists of one part dead load, one part live load, and two parts seismic load

For this situation, we introduce the quantity Ps,equiv which is the sum of the service level load components.  For our example:

Ps,equiv = D + L + E

Where

  • D = 1/4 Ps,equiv = 0.25 Ps,equiv
  • L = 1/4 Ps,equiv = 0.25 Ps,equiv
  • E = 2/4 Ps,equiv = 0.50 Ps,equiv

The quantities Pu and Pa can be related to Ps,equiv by a composite load factor (CLF) that is derived from the load combination equations and the relative values of the individual load components.

LRFD ASD
Pu = CLFLRFD*Ps,equiv Pa = CLFASD*Ps,equiv

The composite load factor is then computed for each load case.  The largest CLF will be from the controlling load case. 

For our example, using the LRFD load cases:

  1. Pu = 1.4(0.25 Ps,equiv) = 0.35 Ps,equiv
  2. Pu = 1.2(0.25 Ps,equiv) + 1.6(0.25 Ps,equiv)= 0.70 Ps,equiv
  3. Pu = 1.2(0.25 Ps,equiv) + 0.5(0.25 Ps,equiv)= 0.425 Ps,equiv
  4. Pu = 1.2(0.25 Ps,equiv) + 0.5(0.25 Ps,equiv)= 0.425 Ps,equiv
  5. Pu = 1.2(0.25 Ps,equiv) + 1.0(0.50 Ps,equiv) + 0.5(0.25 Ps,equiv)= 0.925 Ps,equiv
  6. Pu = 0.9(0.25 Ps,equiv) + 1.0(0.50 Ps,equiv)= 0.725 Ps,equiv

The controlling CLFLRFD in this case is from LRFD LC5 and is 0.925.  With the CLFLRFD we can now find the allowable magnitudes of D, L, and E.

Maximum Pu = 0.925 Ps,equiv < fPn
Ps,equiv < (fPn)/0.925

From this we can compute the service level magnitudes for D, L, and E, by substituting [(fPn)/0.925] in for Ps,equiv.

D < 0.25 [(fPn)/0.925]
L < 0.25 [(fPn)/0.925]
E < 0.50 [(fPn)/0.925]

Doing same thing for the eight ASD load combinations equations listed in the SCM we get:

  1. Pa = (0.25 Ps,equiv) = 0.25 Ps,equiv
  2. Pa = (0.25 Ps,equiv) + (0.25 Ps,equiv)= 0.50 Ps,equiv
  3. Pa = (0.25 Ps,equiv) = 0.25 Ps,equiv
  4. Pa = (0.25 Ps,equiv) + 0.75(0.25 Ps,equiv)= 0.4375 Ps,equiv
  5. Pa = (0.25 Ps,equiv) + 0.70(0.50 Ps,equiv) = 0.60 Ps,equiv
  6. Pa = 0.90(0.25 Ps,equiv) + 0.75(0.50 Ps,equiv) + 0.75(0.25 Ps,equiv)= 0.70 Ps,equiv
  7. Pa = 0.60(0.25 Ps,equiv) = 0.60 Ps,equiv
  8. Pa = 0.60(0.25 Ps,equiv) + 0.70(0.50 Ps,equiv) = 0.50 Ps,equiv

The controlling CLFASD in this case is from ASD LC6 and is 0.70.  With the CLFASD we can now find the allowable magnitudes of D, L, and E.

0.70 Ps,equiv < Pn/ W
Ps,equiv < (Pn/ W)/0.70

From this we can compute the service level magnitudes for D, L, and E:

D < 0.25 (Pn/ W)/0.70
L < 0.25 (Pn/ W)/0.70
E < 0.50 (Pn/ W)/0.70

The controlling composite load factor, CLFASD, can be easily computed using the same spreadsheet you would use for computing all the load combinations simply by putting in the coefficients for the various load types in a single load source column. 

Comparing ASD vs. LRFD Loads

Consider a steel tension member that has a nominal axial capacity, Pn, and is subjected to a combination of dead and live loads.  We will use f = 0.9 and W = 1.67 for now.

The LRFD and ASD factored loads are not directly comparable as the combination equations use different load factors in each case.  We can compare them at service levels by computing an equivalent service load from each combination.

For this problem, Ps,equiv equals the algebraic sum of D and L:  Ps,equiv = D + L

ASD

The controlling ASD load combination equation in this case is ASD-LC2:

Pa = 1.0*D +1.0*L = 1.0*(D+L) = 1.0*Ps,equiv

We can now determine the equivalent total load allowed by ASD by using the design inequality:

Ps,equiv < Pn/W

Ps,equiv < Pn/1.67 = 0.60 Pn

Ps,equiv / Pn < 0.60

LRFD

The controlling LRFD load combination equation in this case is LRFD-LC2:

Pu = 1.2D +1.6L

We make the following definitions:

D = (X%)Ps,equiv
L = (1-X%)Ps,equiv

Where X is the percentage of Ps,equiv that is dead load.  Substituting these definitions into the load combination equation you get:

Pu = 1.2(X)Ps,equiv+1.6(1-X)Ps,equiv = [1.6 - 0.4X]Ps,equiv

Ps,equiv = Pu/[1.6-0.4X]

The term, [1.6 - 0.4X] is a composite load factor that is dependent on the proportion of dead load that makes up the service load.  Similar "composite load factors" can be developed for other load combination equations.

Substituting the above expression into the LRFD version of the design inequality, we get

Pu < fPn

[1.6 - 0.4X]Ps,equiv < fPn

Ps,equiv < fPn / [1.6 - 0.4X]

Ps,equiv < 0.90 Pn / [1.6 - 0.4X]

Ps,equiv / Pn < 0.90 / [1.6 - 0.4X]

Comparison

We can now compare the results by graphing the resulting equations for Ps,equiv/ Pn.  Figure 2.3.1 shows the compared load limits based on percentage dead load.

Figure 2.3.1
Comparison of LRFD & ASD Results

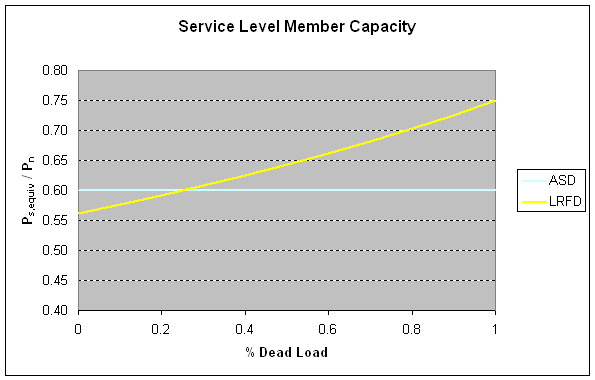From Figure 2.3.1 you can see that, for this case, whenever the total service load is 25% dead load or less that the AISC ASD method gives greater capacity (i.e. it allows more actual load on the structure).  Otherwise the AISC LRFD method is advantageous.

The variable factor of safety associated with the LRFD method is considered to be more consistent with probability since structures that have highly predictable loads (i.e. a large portion of the total load is dead load in this case) don't require the same factor of safety as structures subjected to loads that are not very predictable (such as live load in this case).  So, in the given case, a structure that is subjected to predominately live loads (D < 25% of total load) requires a greater factor of safety than is provided by the ASD method. 

Note that the use of other load combination equations will yield different results.